2024-04-11

メモ：Qtのプロジェクトについて

ディレクトリ構成について

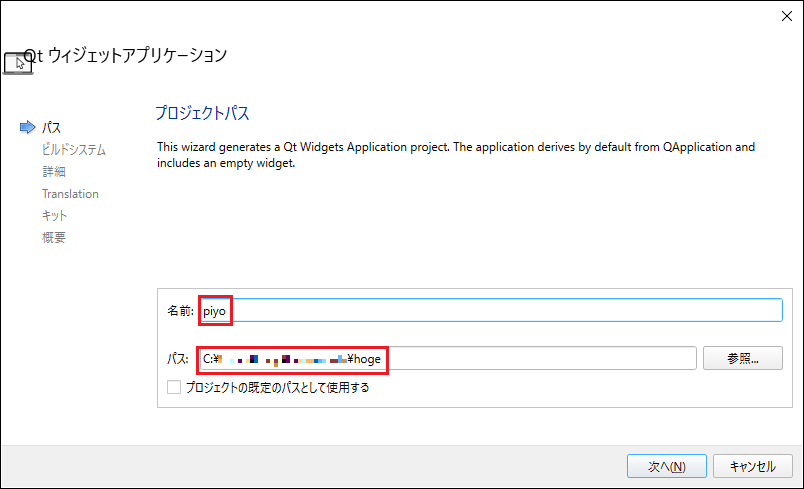
プロジェクト作成時に例えば上記のように設定すると、ディレクトリ構成は下記のようになる。
ソースディレクトリと同じ階層にビルドディレクトリができることに注意。

hoge
├─ piyo : ソースディレクトリ (プロジェクトファイルやソースファイルなど)
├─ build-piyo-***-Debug   : デバッグビルドの出力先
├─ build-piyo-***-Release : リリースビルドの出力先
└─ build-piyo-***-***     : その他のビルド構成の出力先

プロジェクトファイルについて

CMakeLists.txt : CMakeのビルド設定スクリプト (makeにおけるMakefileのようなもの)
CMakeLists.txt.user : QtプロジェクトのXMLファイル (ビルド構成などの設定ファイル)

CMakeLists.txt.user は、基本的にはバージョン管理から除外するファイルであるが、その名に反してビルド構成などの設定も保存されるので、場合によってはバージョン管理に含める必要がある。ただし、デフォルトではビルドディレクトリのパスが絶対パスで保存されるので注意を要する。(このあたり、しょうじきイケてない仕様だと思う。)

ビルドディレクトリを相対パスで指定する

Qt Creatorでプロジェクトのビルド設定を開き、ビルド構成 (DebugやReleaseなど) ごとにビルドディレクトリの指定を編集する。その際、変数 %{sourceDir} がソースディレクトリのパスになるので、そこからの相対パスを指定する。

参考

2024-04-11

PAGEでPython/TkのGUIデザイン

アプリ開発

やりたいこと

Pythonで簡単なGUIアプリを作りたい。
PythonのGUIツールキットとしては、Tkinterが標準で付属している。
Tkinterは、TkをPythonから使えるようにしたもの。
Tkは古めかしいGUIツールキットだが、簡単なGUIで見た目を気にしないならじゅうぶん使える。
しかしコードで画面をデザインするのは面倒なので、Visual Studioのフォームデザイナーのようなツールがほしい。
そのようなツールとしてPAGEがある。
PAGEは、じゃっかん挙動が怪しかったり、微妙な出来のツールではあるが無いよりはマシと思う。

PAGEのインストール

下記からダウンロードしてインストールする

ショートカットからPAGEが起動できない場合、インストールしたフォルダにある page.bat をエディタで開いてみる。(Windows版の場合)
Python のコマンド名が "python3" になっている。Python3系がデフォルトのPython実行環境になっていて、"python3" が有効なコマンド名でない環境の場合、"python3" を "python" に書き換える。

使い方

起動すると下図のような画面が開く。

ウィンドウが5つに分かれていて不便だが、いちおうフォームデザイナーのような感じで使える。
画面デザインのやり方は見ればだいたい分かる。
ボタンのクリックイベントやチェックボックスの変化イベントなどは、Attribute Editor(VSのプロパティウィンドウみたいなやつ) の command に関数名を書くとひな型が自動生成される。
その他のイベントの紐づけは、ウィジェット(たとえばボタン)を右クリックして、「Binding」から関数名を設定する。

メニューの「Gen-Python」から ①「Generate Python GUI」と ②「Generate Support Module」でそれぞれPythonコードを生成して Saveする。

①がGUIデザインのコード、②がメイン関数とイベントハンドラのひな型である。
あとは②にコードを追加していく。

注意点＆挙動の怪しさ

コードを再生成すると手書きのコードは消えてしまうので、バージョン管理ツールなどを利用して手動でマージする
変な状態にはまってしまってPAGEを終了できないことがある？その時はタスクバーから全てのウインドウを閉じる。
Attribute Editorでの設定がコードに反映されないことがある？その時は手動でコードを修正する。

2024-04-07

多角形に関する計算

Python プログラミング

ソース全文はこちら → 多角形に関する計算 · GitHub

凸多角形か判定

# 凸多角形か判定
def isConvex(polygon):
    # n角形
    n = len(polygon)
    # 時計回りまたは反時計回りで、隣接する辺のベクトルのクロス積がすべて同符号なら凸多角形
    cp0 = 0
    for i in range(n):
        p1 = polygon[i]
        p2 = polygon[(i + 1) % n]
        p3 = polygon[(i + 2) % n]
        v21 = p2 - p1
        v32 = p3 - p2
        cp = v21[0] * v32[1] - v21[1] * v32[0]
        if i == 0: cp0 = cp
        elif cp0 * cp < 0:
            return False
    return True

凸多角形の内部か判定

# 凸多角形の内部か判定
def isInConvex(polygon, point):
    # n角形
    n = len(polygon)
    # 時計回りまたは反時計回りで、辺のベクトルと頂点から点のベクトルのクロス積がすべて同符号なら内部の点
    cp0 = 0
    for i in range(n):
        p1 = polygon[i]
        p2 = polygon[(i + 1) % n]
        p3 = point
        v21 = p2 - p1
        v31 = p3 - p1
        cp = v21[0] * v31[1] - v21[1] * v31[0]
        if i == 0: cp0 = cp
        elif cp0 * cp < 0:
            return False
    return True

点から多角形までの最短距離

# 点から多角形までの最短距離
def distance_to_poligon(polygon, point):
    # n角形
    n = len(polygon)
    # 各辺と点の距離の最小値
    for i in range(n):
        p1 = polygon[i]
        p2 = polygon[(i + 1) % n]
        p3 = point
        _d, _p4 = distance_to_segment(p1, p2, p3)
        if  i == 0 or _d < d:
            d = _d
            p4 = _p4
    return d, p4

# 点P3から線分V21までの最短距離dと最近傍点P4
def distance_to_segment(p1, p2, p3):
    v31 = p3 - p1
    v21 = p2 - p1
    v12 = p1 - p2
    v32 = p3 - p2
    # P1が最近傍点の場合
    if np.dot(v31, v21) < 0:
        d = norm(v31)
        p4 = p1
    # P2が最近傍点の場合
    elif np.dot(v32, v12) < 0:
        d = norm(v32)
        p4 = p2
    # P3からV21におろした垂点が最近傍点の場合
    else:
        p41_norm = np.dot(v31, v21) / norm(v21)
        p4 = p1 + v21 / norm(v21) * p41_norm
        d = norm(p3 - p4)
    return d, p4

2024-04-06

金田一耕助と浅見光彦を隔てるもの

切り抜き帖

「開発は、進むほど湖を汚したんですねえ。」
「今だから言えることです。貧しさから豊かさに向かうとき、日本じゅう政治も一人一人の暮らしも、豊かさを求めたでしょう。」
『琵琶湖周航殺人歌』(1990年, 水谷豊版「浅見光彦ミステリー8」より)

金田一耕助と浅見光彦を隔てるものは高度経済成長だと思う。滅びゆく古き日本を看取るのが金田一。すでに忘れられつつある古き日本を訪ねるのが光彦。
横溝正史の金田一耕助シリーズは主に戦後間もない昭和20年代ごろを舞台としており、封建的支配階級の宿業と破滅が描かれる。対して内田康夫の浅見光彦シリーズの代表作は主にバブル経済期前後に書かれており、当時すでに風化しつつあった戦前戦後のできごとが因縁として語られる。

2024-04-06

強者の論理について

切り抜き帖

大河ドラマ『花の乱』(1994年)・第23回「密命」より

畠山義就「三郎、ここがどこだか分かるか？」
伊吹三郎「右衛門佐殿(畠山義就)の陣屋と心得まするが？」
畠山義就「たしかにわしの陣屋だが、つい先ごろまでは上皇様がお住まいあそばされていた仙洞御所だぞ。
　　そしてここには上皇様がお座りあそばされていた。今その席にわしがあぐらをかいて座っているのだ。
　　お主が公家の領主に忠義を尽くしたとて、それには何の意味もない。
　　それもこれもこの度の大乱(応仁の乱)のおかげだ。
　　分かるか？元をたどれば次期将軍の跡目をめぐって御所様(足利義政)と御台様(日野富子)、
　　細川右京太夫殿(細川勝元)と山名宗全入道殿の確執によって引き起こされたものだが、
　　肝心なことは、この大乱を契機として、人の世の全ての価値を変えてしまうことだ。
　　絶対であったものを覆し、真に力のある者どうしがしのぎを削って天下を取りあう。
　　古き殻を破って、新しい力の時代に導く、そのための破壊、そのための戦だ。」
伊吹三郎「いかにも勇猛をもって聞こえるお方の頼もしきお言葉。
　　ただそのぶん、家を焼かれ田畑を踏み荒らされ、兵糧を搾取され、夫役に駆り出される、
　　抗う武器も持ち合わせぬ民人たちのことは、まるで眼中に無きがごときお言葉とも受け止めまする。」

畠山義就「話はまだ終わっていない。
　　わしがあえて公方様(足利義政)の意向をないがしろにして、
　　勝手に山城の国の守護を名乗った理由は二つある。
　　一つは、今の幕府の名ばかりの権威の衣を引きはがし、
　　公方様の無力を諸国の守護に知らしめること。
　　いま一つは、畠山政長の武力侵攻から山城の国を守ることだ。
　　椿の荘を政長の馬蹄の下に蹂躙されたくなかったら、
　　伊吹三郎、今ここでわしの被官(家来)になれ。
　　わしの被官になるよりほかに椿の荘を守る手立ては無いはずだ。」
伊吹三郎「一つ目のことは信じましょう。
　　しかし二つ目のことは、断じて承服いたしかねまする。
　　まずもって、かかる大乱を引き起こしたのも、将軍継承をめぐるいさかいの他に、
　　こなた様と政長殿との長きにわたる領地争いが元凶にござる。
　　その元凶の一方の主が山城の国に陣取られましては、もう一方のお方が黙っておられるはずがない。
　　都を灰燼に帰した同じ大乱が、今度は山城の国で起こることになる。
　　われら山城の国人にとっては、迷惑千万な話だ。
　　ましてやどちらかの被官となって、かかる無益な争いごとに加担するなど、
　　まっぴらご免こうむりたく存じまする。」

コミック版『Fate/EXTRA』・第13話「理想郷 / utopia」(第3巻収録)より

遠坂「私、見ての通り肉食なの。農場(ファーム)暮らしは性に合わない。」
レオ「ミス遠坂、それはあなたの強さがあってこその生き方です。
　　生きるための戦いを肯定するのもいいでしょう。
　　ですが、あなたはすべての人間に自分と同じ強さを求められますか？」
遠坂「それはー」
レオ「できませんね？
　　あなたは自分の身勝手さも傲慢さもわかっています。
　　だからこそ、その苦しみを共有できないすべての力なき人々に
　　自分と同じ苦悩を負えと強制できない。」

2024-04-02

アフィン変換とホモグラフィ変換

数学プログラミング

アフィン変換とホモグラフィ変換とは？
アフィン変換について
ホモグラフィ変換 (射影変換) について
ホモグラフィ変換の特殊解を解析的に解く
Pythonによる実装例
参考

アフィン変換とホモグラフィ変換とは？

アフィン変換：正方形を任意の平行四辺形に写せる (台形など任意の四角形には写せない)
ホモグラフィ変換：正方形を任意の四角形に写せる

アフィン変換について

3×3の行列で表現できる (実質は2×2の行列と2次の列ベクトルで6変数)
$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
拡大縮小、平行移動、回転、せん断(スキュー) からなる
拡大縮小は対角行列
$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
平行移動は単位行列と列ベクトル
$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
回転は回転行列
$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
せん断は単位三角行列
$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & \tan\theta & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$ 　(x軸方向にせん断)

$\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ \tan\theta & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$ 　(y軸方向にせん断)

ホモグラフィ変換 (射影変換) について

任意の4点 $(x_i, y_i), i∈[0,1,2,3]$ を任意の4点 $(x'_i, y'_i)$ に写す。
$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} X'/W' \\ Y'/W' \end{pmatrix}$

$\begin{pmatrix} X' \\ Y' \\ W' \end{pmatrix} = \begin{pmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
　
※ 行列を定数倍しても同じなので $h_{22} = 1$ となるように正規化している。
式を展開して $(x_i, y_i)$ と $(x'_i, y'_i)$ を代入すると
$\begin{pmatrix} x'_0 \\ y'_0 \\ x'_1 \\ y'_1 \\ x'_2 \\ y'_2 \\ x'_3 \\ y'_3 \end{pmatrix} = \begin{pmatrix} x_0 & y_0 & 1 & 0 & 0 & 0 & -x_0x'_0 & -y_0x'_0 \\ 0 & 0 & 0 & x_0 & y_0 & 1 & -x_0y'_0 & -y_0y'_0 \\ x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1x'_1 & -y_1x'_1 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -x_1y'_1 & -y_1y'_1 \\ x_2 & y_2 & 1 & 0 & 0 & 0 & -x_2x'_2 & -y_2x'_2 \\ 0 & 0 & 0 & x_2 & y_2 & 1 & -x_2y'_2 & -y_2y'_2 \\ x_3 & y_3 & 1 & 0 & 0 & 0 & -x_3x'_3 & -y_3x'_3 \\ 0 & 0 & 0 & x_3 & y_3 & 1 & -x_3y'_3 & -y_3y'_3 \end{pmatrix}\begin{pmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \end{pmatrix}$ …①
　
これの逆行列を求めるとホモグラフィ変換行列 H が得られる。
$\begin{pmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \end{pmatrix} = \begin{pmatrix} x_0 & y_0 & 1 & 0 & 0 & 0 & -x_0x'_0 & -y_0x'_0 \\ 0 & 0 & 0 & x_0 & y_0 & 1 & -x_0y'_0 & -y_0y'_0 \\ x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1x'_1 & -y_1x'_1 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -x_1y'_1 & -y_1y'_1 \\ x_2 & y_2 & 1 & 0 & 0 & 0 & -x_2x'_2 & -y_2x'_2 \\ 0 & 0 & 0 & x_2 & y_2 & 1 & -x_2y'_2 & -y_2y'_2 \\ x_3 & y_3 & 1 & 0 & 0 & 0 & -x_3x'_3 & -y_3x'_3 \\ 0 & 0 & 0 & x_3 & y_3 & 1 & -x_3y'_3 & -y_3y'_3 \end{pmatrix}^{-1}\begin{pmatrix} x'_0 \\ y'_0 \\ x'_1 \\ y'_1 \\ x'_2 \\ y'_2 \\ x'_3 \\ y'_3 \end{pmatrix}$ …②

ホモグラフィ変換の特殊解を解析的に解く

たいていの用途では、写像元/写像先のいずれか一方は、x軸とy軸に平行な長方形であり、これは単位正方形に正規化できる。この場合、①の方程式はかなり簡単になる。
$(x_0, y_0), (x_1, y_1), (x_2, y_2), (x_3, y_3) = (0, 0), (1, 0), (1, 1), (0, 1)$ とすると

$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & -x'_1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & -y'_1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & -x'_2 & -x'_2 \\ 0 & 0 & 0 & 1 & 1 & 1 & -y'_2 & -y'_2 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & -x'_3 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & -y'_3 \end{pmatrix} \begin{pmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \end{pmatrix} = \begin{pmatrix} x'_0 \\ y'_0 \\ x'_1 \\ y'_1 \\ x'_2 \\ y'_2 \\ x'_3 \\ y'_3 \end{pmatrix}$ …③
これを解くと
$h_{02} = x'_0 　, 　h_{12} = y'_0$

$A = x'_1 - x'_2 , 　B = x'_3 - x'_2 , 　C = x'_0 - x'_1 + x'_2 - x'_3$
$D = y'_1 - y'_2 , 　E = y'_3 - y'_2 , 　F = y'_0 - y'_1 + y'_2 - y'_3$
$h_{20} = \dfrac{CE - BF}{AE - BD}　, 　h_{21} = \dfrac{AF - CD}{AE - BD}$

$h_{00} = x'_1 - x'_0 + x'_1 h_{20}$
$h_{10} = y'_1 - y'_0 + y'_1 h_{20}$
$h_{01} = x'_3 - x'_0 + x'_3 h_{21}$
$h_{11} = y'_3 - y'_0 + y'_3 h_{21}$
　
※計算メモ → メモ1, メモ2
逆に単位正方行列への変換であれば上記のホモグラフィ行列 H の逆行列を用いればよい。( H は3×3行列であるから公式で計算すればよい。)
行列計算のライブラリを利用して② の逆行列を数値計算で解けるならそれでもよし。
そのようなライブラリが利用できない環境の場合、ここで述べた特殊解を利用すれば、実装が比較的容易であり、計算量も少なくて済む。

Pythonによる実装例

HomographyTest1.py は ② の逆行列を数値計算で解くやり方
HomographyTest2.py は ③ の解析解を解くやり方

参考

2024-04-01

開発対象システム別の利用言語

切り抜き帖プログラミング

いわゆるプログラミング言語ランキングみたいなやつはぜんぜん意味が無いと思っている。一口にプログラミング言語といっても、分野によって使われる言語の主流がぜんぜんちがうからだ。

開発対象システム別の利用言語の比率というデータを見かけた。(これもやや疑問があるけど)

組込み系：もちろん C/C++ が圧倒的。まあ他の言語じゃ無理だし。(Rust来ないなぁ)
データ分析 / AI：やはり Python が圧倒的。ここまで圧倒的なのか。
スマホアプリ：もちろん Java/Kotlin と Swift/Objective-C が強いけど、C# や JavaScript もそこそこ。
Web系：JavaScript/TypeScriptとPHPが多いけど、かなり分かれる。
(Javaがなぜここに？ PHPはフロントエンドじゃないだろ、バックエンドも含むならRubyは？)
業務系：Java と C# が多いけど、かなり分かれる。